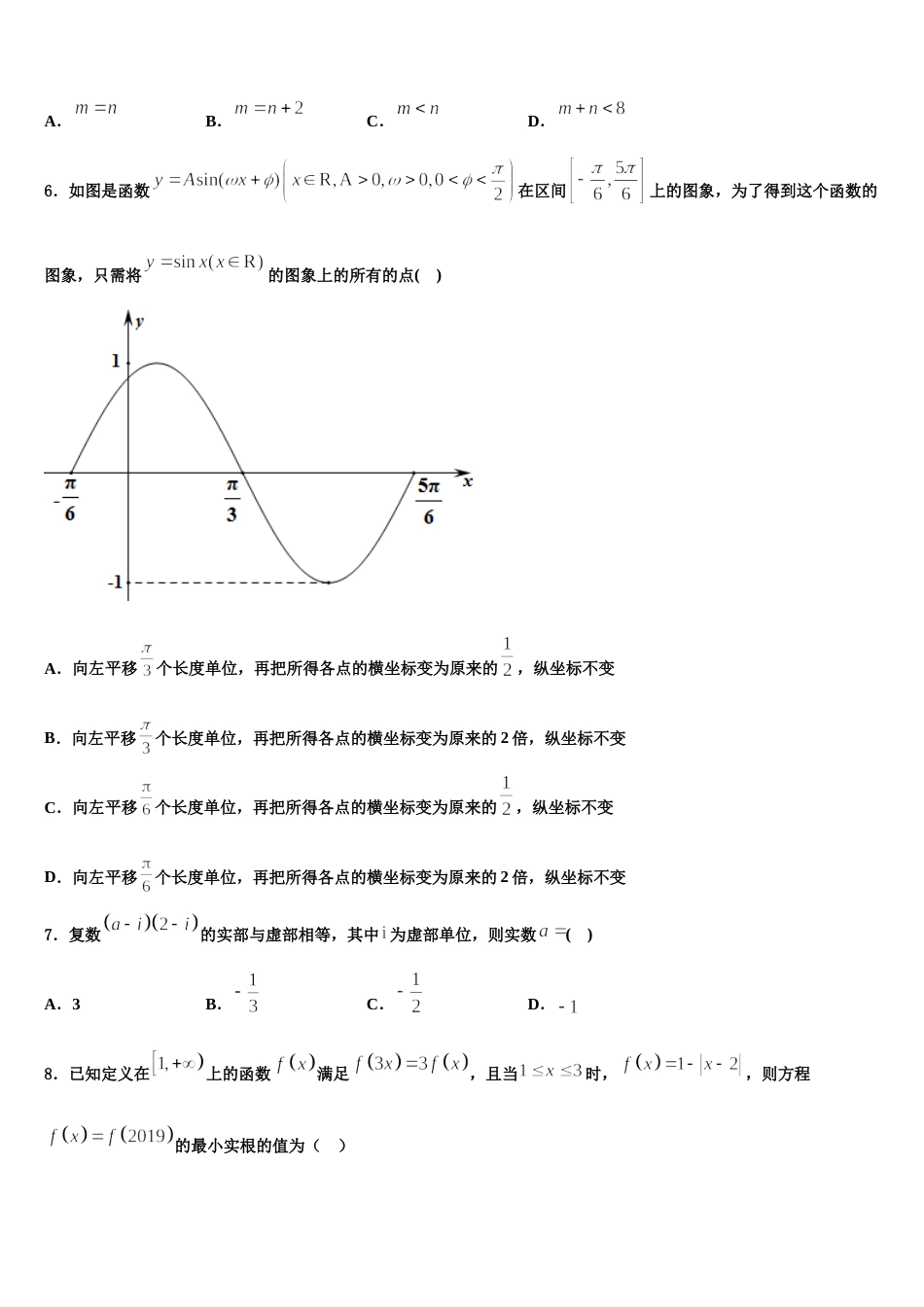
甘肃省河西五市部分普通高中 2023-2024 学年高三二诊模拟考试数学试卷请考生注意:1.请用 2B 铅笔将选择题答案涂填在答题纸相应位置上,请用 0.5 毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知命题,;命题若,则,下列命题为真命题的是( )A.B.C.D.2.从抛物线上一点 (点在轴上方)引抛物线准线的垂线,垂足为,且,设抛物线的焦点为,则直线的斜率为( )A.B.C.D.3.已知集合,则( )A.B.C.D.4.已知类产品共两件,类产品共三件,混放在一起,现需要通过检测将其区分开来,每次随机检测一件产品,检测后不放回,直到检测出 2 件类产品或者检测出 3 件类产品时,检测结束,则第一次检测出类产品,第二次检测出类产品的概率为( )A.B.C.D.5.如图,正方体的底面与正四面体的底面在同一平面上,且,若正方体的六个面所在的平面与直线相交的平面个数分别记为,则下列结论正确的是( )A.B.C.D.6.如图是函数在区间上的图象,为了得到这个函数的图象,只需将的图象上的所有的点( )A.向左平移个长度单位,再把所得各点的横坐标变为原来的,纵坐标不变B.向左平移个长度单位,再把所得各点的横坐标变为原来的 2 倍,纵坐标不变C.向左平移个长度单位,再把所得各点的横坐标变为原来的,纵坐标不变D.向左平移个长度单位,再把所得各点的横坐标变为原来的 2 倍,纵坐标不变7.复数的实部与虚部相等,其中 为虚部单位,则实数( )A.3B.C.D.8.已知定义在上的函数满足,且当时,,则方程的最小实根的值为( )A.B.C.D.9.已知非零向量满足,若夹角的余弦值为,且,则实数的值为( )A.B.C.或D.10.已知命题:使成立. 则为( )A.均成立B.均成立C.使成立D.使成立11.在棱长均相等的正三棱柱中,为的中点,在上,且,则下述结论:①;②;③平面平面:④异面直线与所成角为其中正确命题的个数为( )A.1B.2C.3D.412.在原点附近的部分图象大概是( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.在中,角的对边分别为,且.若为钝角,,则的面积为____________.14.将 2 个相同的红球和 2 个相同的黑球全部放入甲、乙、丙、丁四个盒子里,其中甲、乙盒子均最多可放入 2 个球,丙、丁盒子均最多可放入 1 个球,且不同颜色的球不能放入同一个盒子里,共有________种不同的放法.15.定义在封闭的平面区域内任意两点的距离的最大值称为平面区域的“直径”.已知锐角三角形的三个点,,,在半径为的圆上,且,分别以各边为直径向外作三个半圆,这三个半圆和构成平面区域,则平面区域的“直径”的最大值是__________.16.已知抛物线的焦点为,斜率为 2 的直线 与的交点为,若,则直线 的方程为___________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)如图所示,三棱柱中,平面,点,分别在线段,上,且,,是线段的中点.(Ⅰ)求证:平面;(Ⅱ)若,,,求直线与平面所成角的正弦值.18.(12 分)在中,角的对边分别为,已知.(1)求角的大小;(2)若,求的面积.19.(12 分)在极坐标系中,直线 的极坐标方程为,以极点为原点,极轴为轴的正半轴建立平面直角坐标系,曲线的参数方程为(为参数),求直线 与曲线的交点的直角坐标.20.(12 分)已知函数.( ) Ⅰ 求函数的单调区间;() Ⅱ 当时,求函数在上最小值.21.(12 分)设函数,,(Ⅰ)求曲线在点(1,0)处的切线方程;(Ⅱ)求函数在区间上的取值范围.22.(10 分)a,b,c 分别为△ABC 内角 A,B,C 的对边.已知 a=3,,且 B=60°.(1)求△ABC 的面积; (2)若 D,E 是 BC 边上的三等分点,求.参考答案一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一...