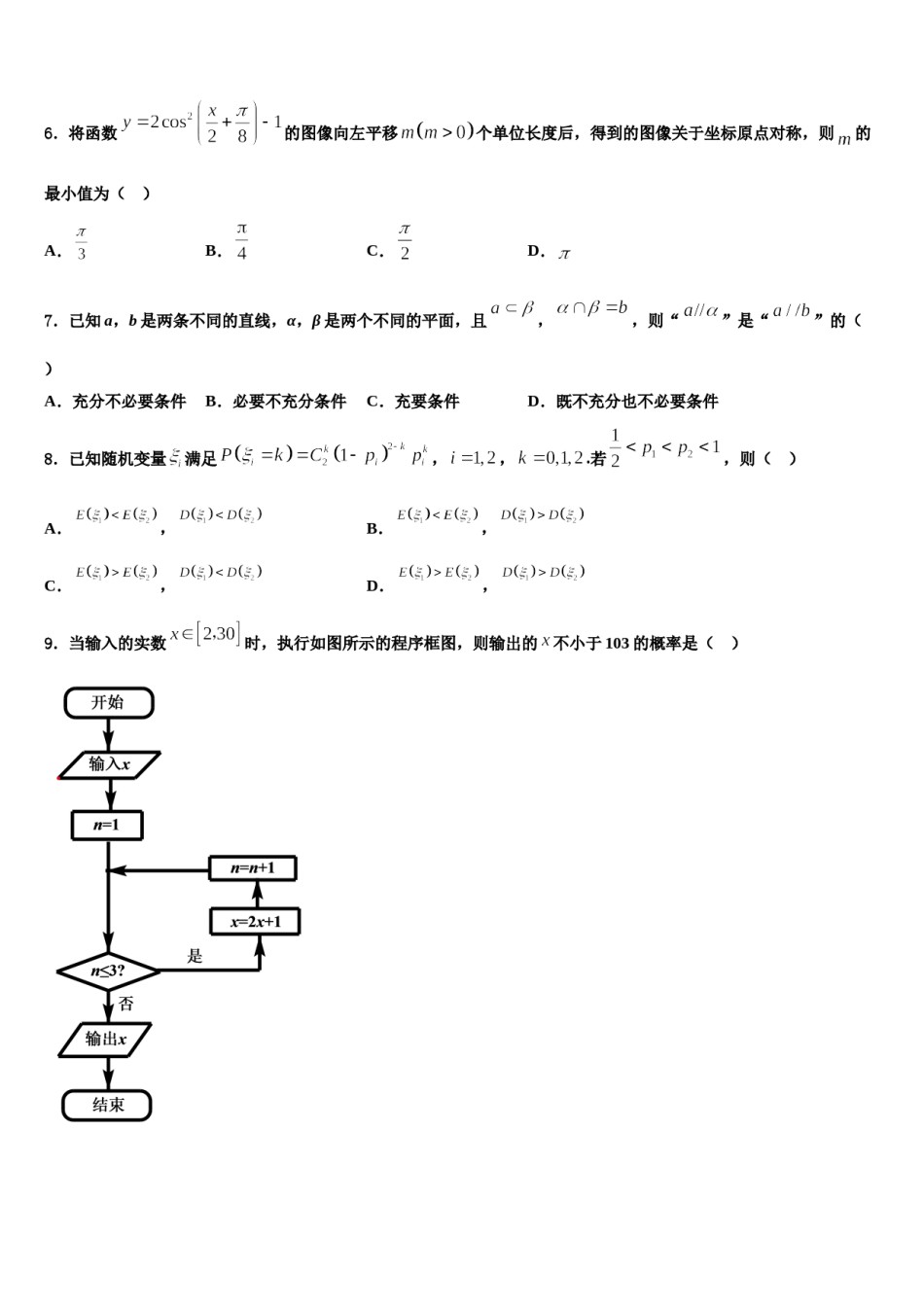
西安市东仪中学2023-2024学年高三第二次诊断性检测数学试卷注意事项:1.答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.设过抛物线上任意一点(异于原点)的直线与抛物线交于两点,直线与抛物线的另一个交点为,则()A.2.已知数列B.C.D.A.3.已知点是公比为的等比数列,且,若数列是递增数列,则的取值范围为()A.6B.C.D.,若点在曲线上运动,则面积的最小值为()B.3C.D.4.若双曲线的离心率,则该双曲线的焦点到其渐近线的距离为()A.5.已知椭圆B.2C.D.1的短轴长为2,焦距为分别是椭圆的左、右焦点,若点为上的任意一点,则的取值范围为()A.B.C.D.6.将函数的图像向左平移个单位长度后,得到的图像关于坐标原点对称,则的C.D.最小值为()A.B.7.已知a,b是两条不同的直线,α,β是两个不同的平面,且,,则“”是“”的()B.必要不充分条件C.充要条件D.既不充分也不必要条件A.充分不必要条件8.已知随机变量满足,,.若,则()A.,B.,C.,D.,9.当输入的实数时,执行如图所示的程序框图,则输出的不小于103的概率是()A.B.C.D.10.命题:的否定为A.B.C.D.11.已知,满足条件(为常数),若目标函数的最大值为9,则()A.B.C.D.12.在“一带一路”知识测验后,甲、乙、丙三人对成绩进行预测.甲:我的成绩比乙高.乙:丙的成绩比我和甲的都高.丙:我的成绩比乙高.成绩公布后,三人成绩互不相同且只有一个人预测正确,那么三人按成绩由高到低的次序为A.甲、乙、丙B.乙、甲、丙C.丙、乙、甲D.甲、丙、乙二、填空题:本题共4小题,每小题5分,共20分。13.已知抛物线的焦点为,过点且斜率为1的直线与抛物线交于点,以线段为直径的圆上存在点,使得以为直径的圆过点,则实数的取值范围为________.14.函数的定义域为____.15.在边长为2的正三角形中,,则的取值范围为______.16.曲线在点处的切线方程为______.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)在平面直角坐标系中,曲线的参数方程为(为参数).以坐标原点为极点,轴正半轴为极轴建立极坐标系,直线的极坐标方程为.(Ⅰ)求直线的直角坐标方程与曲线的普通方程;(Ⅱ)已知点设直线与曲线相交于两点,求的值.18.(12分)如图,在斜三棱柱中,平面平面,,,,均为正三角形,E为AB的中点.(Ⅰ)证明:平面;(Ⅱ)求斜三棱柱截去三棱锥后剩余部分的体积.19.(12分)在中,内角A,B,C的对边分别为a,b,c,且满足.(1)求B;(2)若,AD为BC边上的中线,当的面积取得最大值时,求AD的长.20.(12分)如图,在棱长为的正方形中,,分别为,边上的中点,现以为折痕将点旋转至点的位置,使得为直二面角.(1)证明:;(2)求与面所成角的正弦值.21.(12分)已知,,分别为内角,,的对边,且.,角为钝角,(1)证明:;(2)若的面积,,求角.22.(10分)在三角形ABC中,角A,B,C的对边分别为a,b,c,若(1)求的值;(2)求边的长.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、C【解析】画出图形,将三角形面积比转为线段长度比,进而转为坐标的表达式。写出直线方程,再联立方程组,求得交点坐标,最后代入坐标,求得三角形面积比.【详解】作图,设与的夹角为,则中边上的高与中边上的高之比为,,设,则直线,即,与联立,解得,从而得到面积比为.故选:【点睛】解决本题主要在于将面积比转化为线段长的比例关系,进而联立方程组求解,是一道不错的综合题.2、D【解析】先根据已知条件求解出的通项公式,然后...