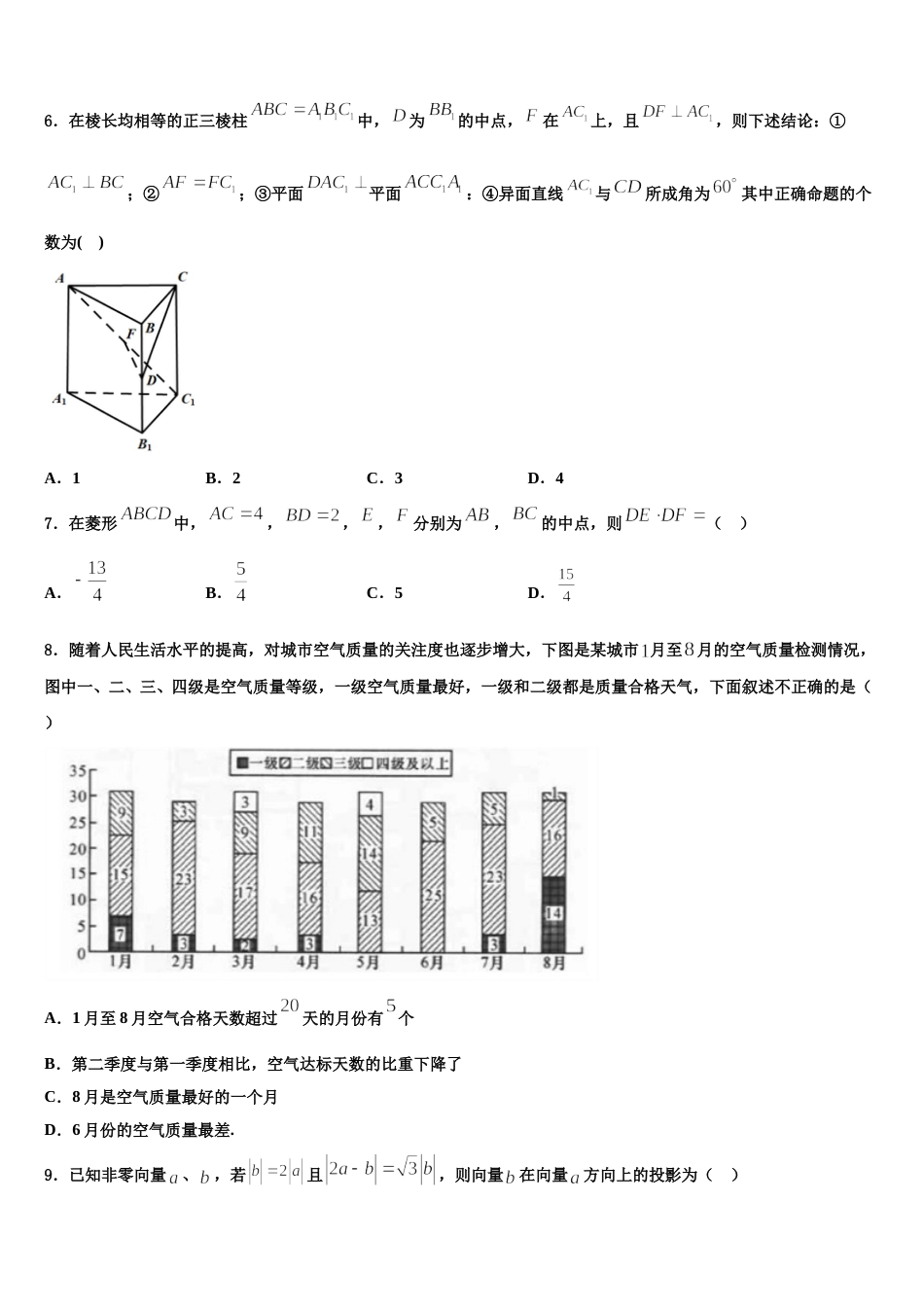
西藏林芝地区二高 2024 年高三第二次诊断性检测数学试卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.关于函数,下列说法正确的是( )A.函数的定义域为B.函数一个递增区间为C.函数的图像关于直线对称D.将函数图像向左平移个单位可得函数的图像2.设等比数列的前项和为,则“”是“”的( )A.充分不必要B.必要不充分C.充要D.既不充分也不必要3.一只蚂蚁在边长为的正三角形区域内随机爬行,则在离三个顶点距离都大于的区域内的概率为( )A.B.C.D.4.设为定义在上的奇函数,当时,(为常数),则不等式的解集为( )A.B.C.D.5.已知复数 z=(1+2i)(1+ai)(a∈R),若 z∈R,则实数 a=( )A.B.C.2D.﹣26.在棱长均相等的正三棱柱中,为的中点,在上,且,则下述结论:①;②;③平面平面:④异面直线与所成角为其中正确命题的个数为( )A.1B.2C.3D.47.在菱形中,,,,分别为,的中点,则( )A.B.C.5D.8.随着人民生活水平的提高,对城市空气质量的关注度也逐步增大,下图是某城市 月至月的空气质量检测情况,图中一、二、三、四级是空气质量等级,一级空气质量最好,一级和二级都是质量合格天气,下面叙述不正确的是( )A.1 月至 8 月空气合格天数超过天的月份有个B.第二季度与第一季度相比,空气达标天数的比重下降了C.8 月是空气质量最好的一个月D.6 月份的空气质量最差.9.已知非零向量、,若且,则向量在向量方向上的投影为( )A.B.C.D.10.设,则“”是“”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件11.给出下列三个命题:①“”的否定;② 在中,“”是“”的充要条件;③ 将函数的图象向左平移个单位长度,得到函数的图象.其中假命题的个数是( )A.0B.1C.2D.312.已知焦点为的抛物线的准线与轴交于点,点在抛物线上,则当取得最大值时,直线的方程为( )A.或B.或C.或D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.过抛物线 C:()的焦点 F 且倾斜角为锐角的直线 l 与 C 交于 A,B 两点,过线段的中点 N且垂直于 l 的直线与 C 的准线交于点 M,若,则 l 的斜率为______.14.已知函数的最大值为 3,的图象与 y 轴的交点坐标为,其相邻两条对称轴间的距离为 2,则15.若,则________.16.若点在直线上,则的值等于______________ .三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)在四棱锥的底面是菱形, 底面,, 分别是的中点,.(Ⅰ)求证: ;(Ⅱ)求直线与平面所成角的正弦值;(III)在边上是否存在点,使与所成角的余弦值为,若存在,确定点的位置;若不存在,说明理由.18.(12 分)已知函数.(1)若在处取得极值,求的值;(2)求在区间上的最小值;(3)在(1)的条件下,若,求证:当时,恒有成立.19.(12 分)在平面直角坐标系中,已知直线 的参数方程为( 为参数)和曲线(为参数),以坐标原点为极点,轴的非负半轴为极轴建立极坐标系.(1)求直线 和曲线的极坐标方程;(2)在极坐标系中,已知点是射线与直线 的公共点,点是与曲线的公共点,求的最大值.20.(12 分)在中,角、、的对边分别为、、,且.(1)若,,求的值;(2)若,求的值.21.(12 分)如图, 在四棱锥中, 底面, ,, ,,点为棱的中点.(1)证明::(2)求直线与平面所成角的正弦值;(3)若为棱上一点, 满足, 求二面角的余弦值.22.(10 分)中国古建筑中的窗饰是艺术和技术的统一体,给人于美的享受.如图(1)为一花窗;图(2)所示是一扇窗中的一格,呈长方形,长 30 cm,宽...