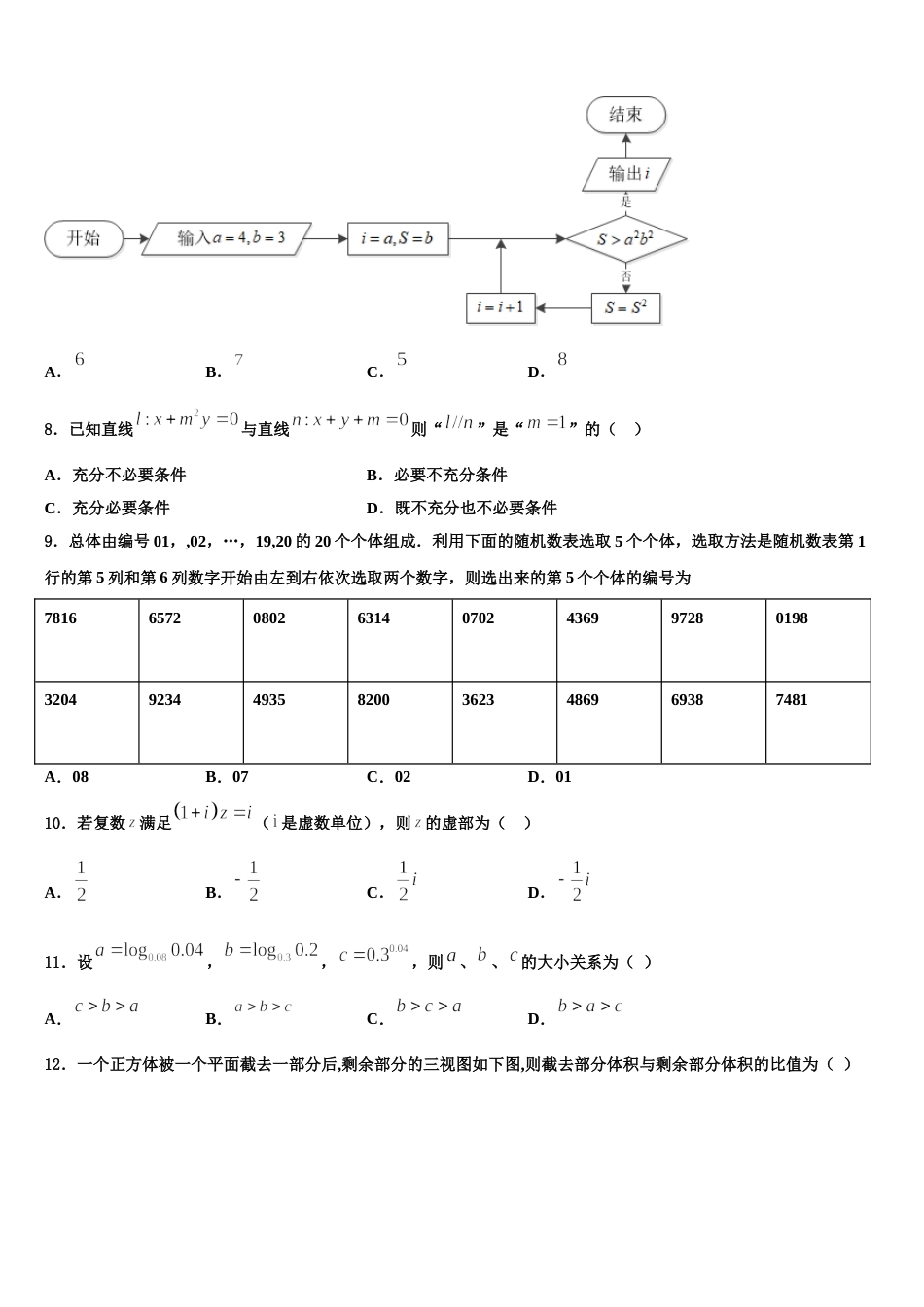
西藏自治区拉萨市西藏自治区拉萨中学 2024 届高考数学必刷试卷注意事项1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用 2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.如图,在平面四边形 ABCD 中,若点 E 为边 CD 上的动点,则的最小值为 ( )A.B.C.D.2.半径为 2 的球内有一个内接正三棱柱,则正三棱柱的侧面积的最大值为( )A.B.C.D.3.如图,正方体的底面与正四面体的底面在同一平面上,且,若正方体的六个面所在的平面与直线相交的平面个数分别记为,则下列结论正确的是( )A.B.C.D.4.已知某几何体的三视图如右图所示,则该几何体的体积为( )A.3B.C.D.5.某四棱锥的三视图如图所示,则该四棱锥的体积为( )A.B.C.D.6.《九章算术》有如下问题:“今有金箠,长五尺,斩本一尺,重四斤;斩末一尺,重二斤,问次一尺各重几何?”意思是:“现在有一根金箠, 长五尺在粗的一端截下一尺,重斤;在细的一端截下一尺,重斤,问各尺依次重多少?”按这一问题的颗设,假设金箠由粗到细各尺重量依次成等差数列,则从粗端开始的第二尺的重量是( )A.斤B. 斤C.斤D.斤7.如图所示的程序框图,若输入,,则输出的结果是( )A.B.C.D.8.已知直线与直线则“”是“”的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件9.总体由编号 01,,02,…,19,20 的 20 个个体组成.利用下面的随机数表选取 5 个个体,选取方法是随机数表第 1行的第 5 列和第 6 列数字开始由左到右依次选取两个数字,则选出来的第 5 个个体的编号为7816657208026314070243699728019832049234493582003623486969387481A.08B.07C.02D.0110.若复数满足( 是虚数单位),则的虚部为( )A.B.C.D.11.设,,,则、、的大小关系为( )A.B.C.D.12.一个正方体被一个平面截去一部分后,剩余部分的三视图如下图,则截去部分体积与剩余部分体积的比值为( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知向量,,若,则________.14.某外商计划在个候选城市中投资 个不同的项目,且在同一个城市投资的项目不超过个,则该外商不同的投资方案有____种.15.如图,两个同心圆的半径分别为和,为大圆的一条 直径,过点作小圆的切线交大圆于另一点,切点为,点为劣弧上的任一点(不包括 两点),则的最大值是__________.16.定义在上的偶函数满足,且,当时,.已知方程在区间上所有的实数根之和为.将函数的图象向右平移个单位长度,得到函数的图象,则__________,__________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)在平面直角坐标系中,设,过点的直线 与圆相切,且与抛物线相交于两点.(1)当在区间上变动时,求中点的轨迹;(2)设抛物线焦点为,求的周长(用表示),并写出时该周长的具体取值.18.(12 分)已知函数,(1)证明:在区间单调递减;(2)证明:对任意的有.19.(12 分)如图,在直棱柱中,底面为菱形,,,与相交于点,与相交于点.(1)求证:平面;(2)求直线与平面所成的角的正弦值.20.(12 分)已知函数,.(1)若曲线在点处的切线方程为,求,;(2)当时,,求实数的取值范围.21.(12 分)如图,为等腰直角三角形,,D 为 AC 上一点,将沿 BD 折起,得到三棱锥,且使得在底面 BCD 的投影 E 在线段 BC 上,连接 AE. (1)证明:;(2)若,求二面角的余弦值.22.(10 分)已知在平面直角坐标系中,曲线的参数方程为(为参数.).以坐标原点为极点,轴正半轴为极轴建立极坐标系,直线 的极坐标方程为,曲线与直线 其中的一个交点为,且点极径.极角(1)求曲线的极坐标方程与点的极坐标;(2)已知直线的直角坐标方程为,...