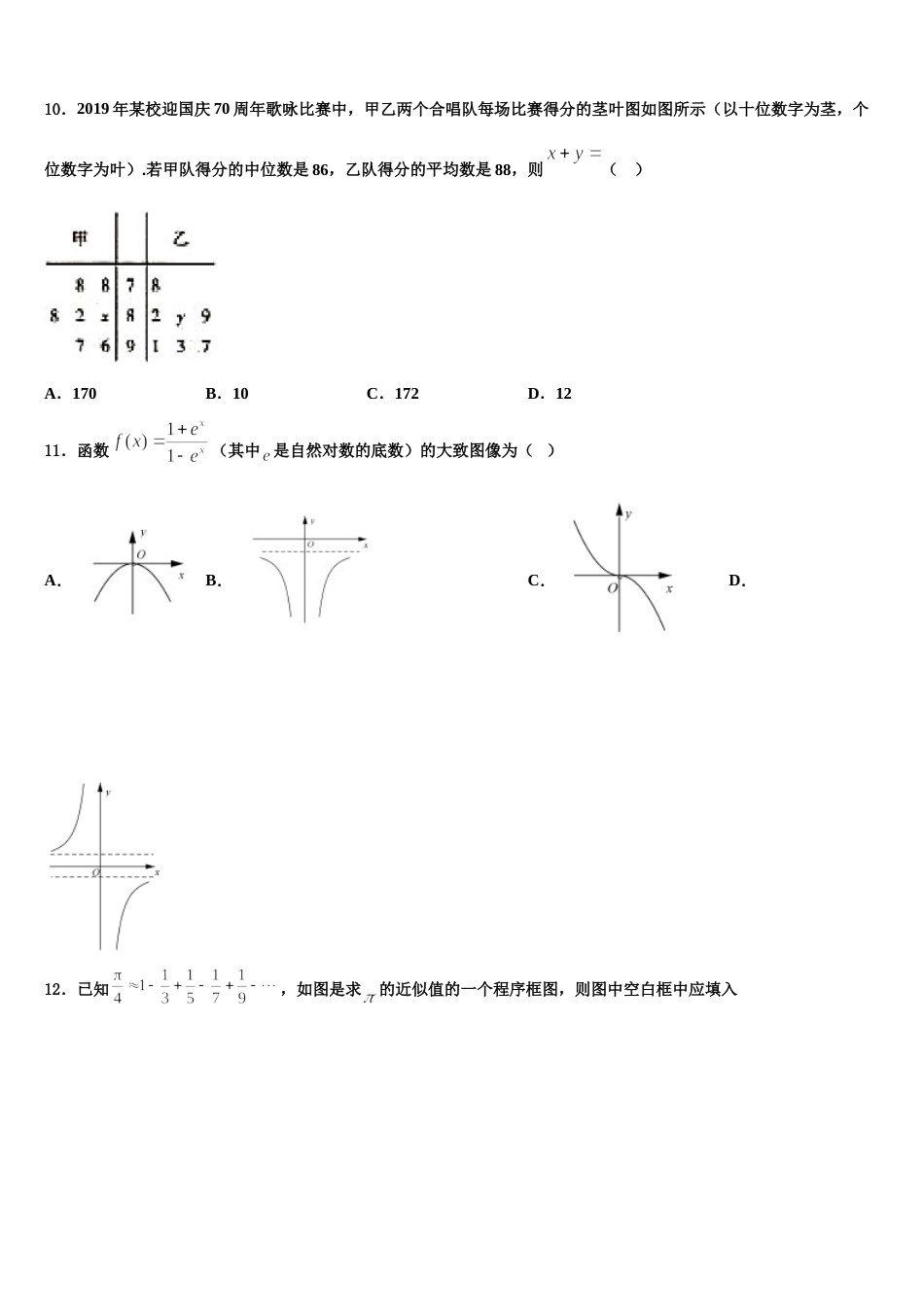
贵州省六盘水市七中 2024 届高三冲刺模拟数学试卷考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.函数在上单调递减,且是偶函数,若 ,则 的取值范围是()A.(2,+∞)B.(﹣∞,1)∪(2,+∞)C.(1,2)D.(﹣∞,1)2.已知函数,为的零点,为图象的对称轴,且在区间上单调,则的最大值是( )A.B.C.D.3.已知函数,为图象的对称中心,若图象上相邻两个极值点,满足,则下列区间中存在极值点的是( )A.B.C.D.4.为比较甲、乙两名高二学生的数学素养,对课程标准中规定的数学六大素养进行指标测验(指标值满分为 5 分,分值高者为优),根据测验情况绘制了如图所示的六大素养指标雷达图,则下面叙述正确的是( )A.乙的数据分析素养优于甲B.乙的数学建模素养优于数学抽象素养C.甲的六大素养整体水平优于乙D.甲的六大素养中数据分析最差5.已知函数满足,设,则“”是“”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6.已知集合,集合,则( )A.B.C.D.7.设某大学的女生体重 y(单位:kg)与身高 x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为=0.85x-85.71,则下列结论中不正确的是A.y 与 x 具有正的线性相关关系B.回归直线过样本点的中心(,)C.若该大学某女生身高增加 1cm,则其体重约增加 0.85kgD.若该大学某女生身高为 170cm,则可断定其体重比为 58.79kg8.设正项等比数列的前 n 项和为,若,,则公比( )A.B.4C.D.29.若点是角的终边上一点,则( )A.B.C.D.10.2019 年某校迎国庆 70 周年歌咏比赛中,甲乙两个合唱队每场比赛得分的茎叶图如图所示(以十位数字为茎,个位数字为叶).若甲队得分的中位数是 86,乙队得分的平均数是 88,则( )A.170B.10C.172D.1211.函数(其中 是自然对数的底数)的大致图像为( )A.B.C.D.12.已知,如图是求的近似值的一个程序框图,则图中空白框中应填入A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.平行四边形中,,为边上一点(不与重合),将平行四边形沿折起,使五点均在一个球面上,当四棱锥体积最大时,球的表面积为________.14.复数(其中 i 为虚数单位)的共轭复数为________.15.设 f(x)=etx(t>0),过点 P(t,0)且平行于 y 轴的直线与曲线 C:y=f(x)的交点为 Q,曲线 C 过点 Q 的切线交 x 轴于点 R,若 S(1,f(1)),则△PRS 的面积的最小值是_____.16.在矩形中,,为的中点,将和分别沿,翻折,使点与重合于点.若,则三棱锥的外接球的表面积为_____.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)如图 1,与是处在同-个平面内的两个全等的直角三角形,,,连接是边上一点,过作,交于点,沿将向上翻折,得到如图 2 所示的六面体(1)求证:(2)设若平面底面,若平面与平面所成角的余弦值为,求的值;(3)若平面底面,求六面体的体积的最大值.18.(12 分)在国家“大众创业,万众创新”战略下,某企业决定加大对某种产品的研发投入.为了对新研发的产品进行合理定价,将该产品按事先拟定的价格试销,得到一组检测数据如表所示:试销价格(元)产品销量 (件)已知变量且有线性负相关关系,现有甲、乙、丙三位同学通过计算求得回归直线方程分别为:甲; 乙;丙,其中有且仅有一位同学的计算结果是正确的.(1)试判断谁的计算结果正确?(2)若由线性回归方程得到的估计数据与检测数据的误差不超过 ,则称该检测数据是“理想数据”,现从检测数据中随机抽取个,...