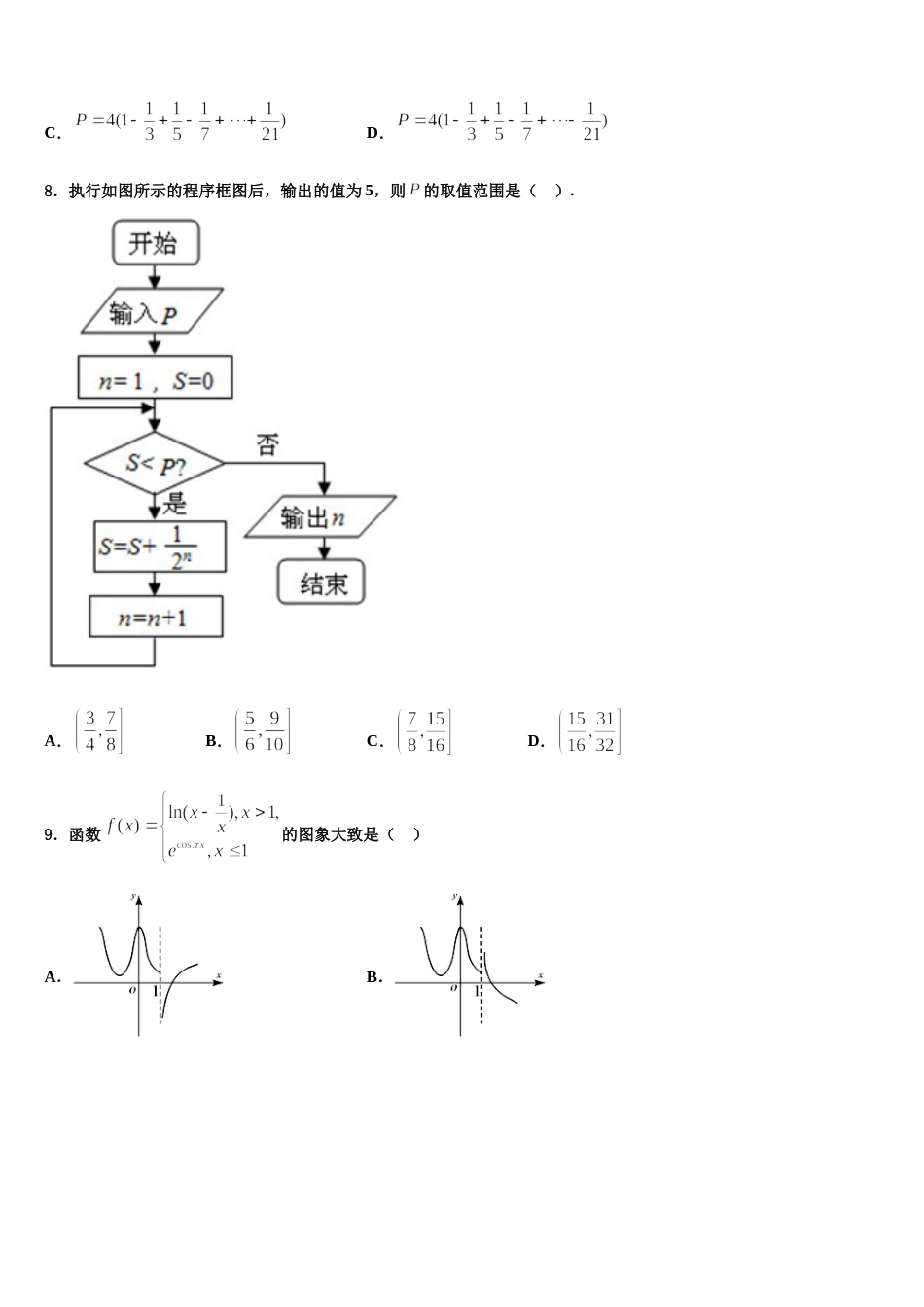
贵州省务川自治县民族寄宿制中学 2023-2024 学年高考冲刺模拟数学试题注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.设函数的导函数,且满足,若在中,,则( )A.B.C.D.2.已知集合,,且、都是全集(为实数集)的子集,则如图所示韦恩图中阴影部分所表示的集合为( )A.B.或C.D.3.函数 的部分图象如图所示,则 ( )A.6B.5C.4D.34.已知函数,.若存在,使得成立,则的最大值为( )A.B.C.D.5.已知集合,则为( )A.[0,2)B.(2,3]C.[2,3]D.(0,2]6.已知集合,,则的真子集个数为( )A.1 个B.2 个C.3 个D.4 个7.德国数学家莱布尼兹(1646 年-1716 年)于 1674 年得到了第一个关于 π 的级数展开式,该公式于明朝初年传入我国.在我国科技水平业已落后的情况下,我国数学家 天文学家明安图、(1692 年-1765 年)为提高我国的数学研究水平,从乾隆初年(1736 年)开始,历时近 30 年,证明了包括这个公式在内的三个公式,同时求得了展开三角函数和反三角函数的 6 个新级数公式,著有《割圆密率捷法》一书,为我国用级数计算 π 开创了先河.如图所示的程序框图可以用莱布尼兹“关于 π 的级数展开式”计算 π 的近似值(其中 P 表示 π 的近似值),若输入,则输出的结果是( )A.B.C.D.8.执行如图所示的程序框图后,输出的值为 5,则的取值范围是( ). A.B.C.D.9.函数的图象大致是( )A.B.C.D.10.在正项等比数列{an}中,a5-a1=15,a4-a2 =6,则 a3=( )A.2B.4C.D.811.函数的图象如图所示,为了得到的图象,可将的图象( )A.向右平移个单位B.向右平移个单位C.向左平移个单位D.向左平移个单位12.某几何体的三视图如图所示,则该几何体的体积为( )A.B.3C.D.4二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知函数的图象在点处的切线方程是,则的值等于__________.14.在中,内角的对边分别是,若,,则____.15.某几何体的三视图如图所示(单位:),则该几何体的体积是_____;最长棱的长度是_____.16.在直角三角形中,为直角,,点在线段上,且,若,则的正切值为_____.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知是圆:的直径,动圆过,两点,且与直线相切.(1)若直线的方程为,求的方程;(2)在轴上是否存在一个定点,使得以为直径的圆恰好与轴相切?若存在,求出点的坐标;若不存在,请说明理由.18.(12 分)已知离心率为的椭圆经过点.(1)求椭圆的方程;(2)荐椭圆的右焦点为,过点的直线与椭圆分别交于,若直线、、的斜率成等差数列,请问的面积是否为定值?若是,求出此定值;若不是,请说明理由.19.(12 分)已知函数.(1)求的单调区间;(2)讨论零点的个数.20.(12 分)已知函数的图象在处的切线方程是.(1)求的值;(2)若函数,讨论的单调性与极值;(3)证明:.21.(12 分)已知函数.(1)当时,求函数的值域.(2)设函数,若,且的最小值为,求实数的取值范围.22.(10 分)在直角坐标系中,曲线的参数方程为(为参数,将曲线经过伸缩变换后得到曲线.在以原点为极点,轴正半轴为极轴的极坐标系中,直线 的极坐标方程为.(1)说明曲线是哪一种曲线,并将曲线的方程化为极坐标方程;(2)已知点是曲线上的任意一点,又直线 上有两点和,且,又点的极角为,点的极角为锐角.求:① 点的极角;②面积的取值范围.参考答案一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、D【解析】根据的结构形式,设,求导,则,在上是增函数,再根据在中,,得到,...