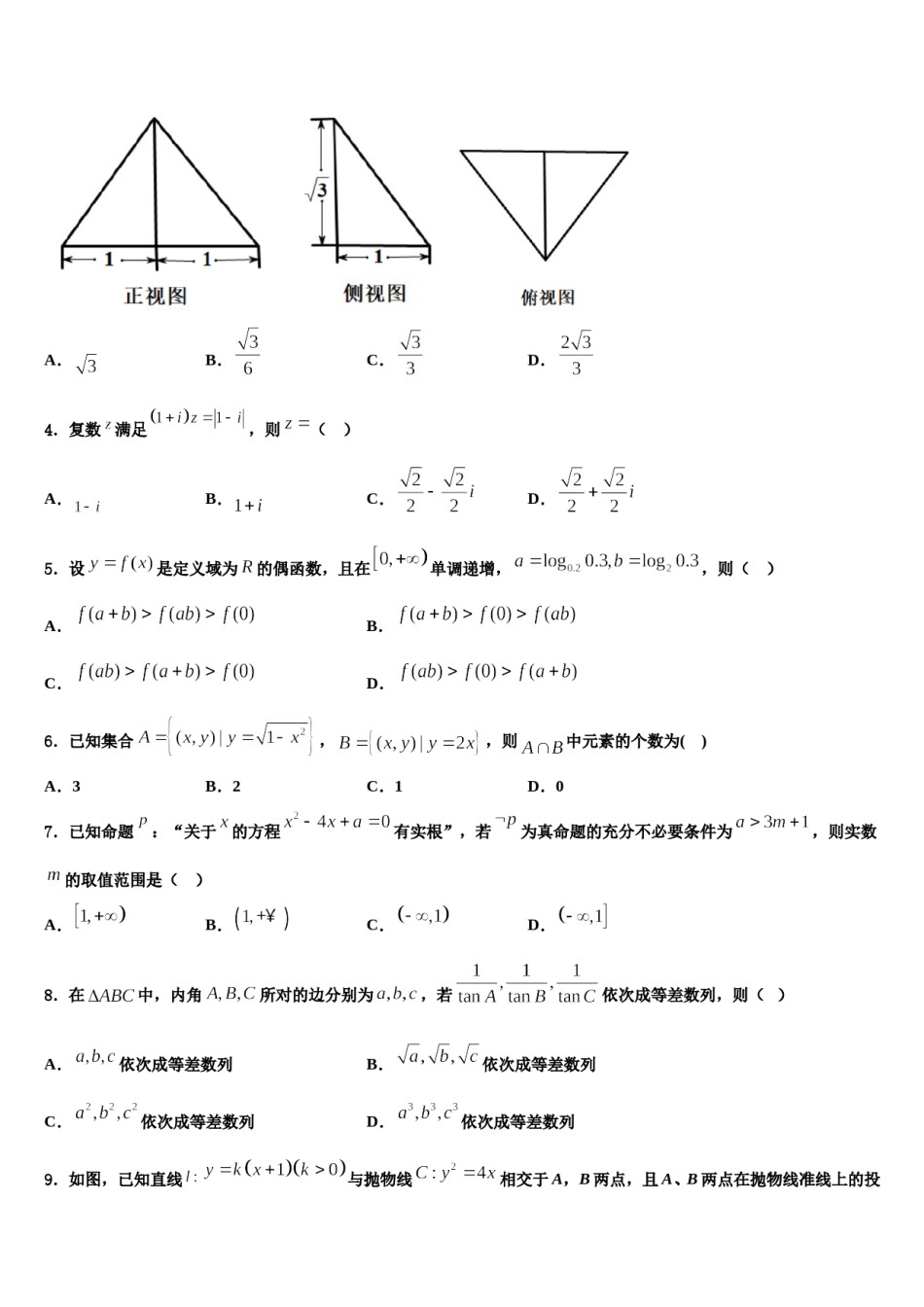
贵港市高级中学2024年高三3月份第一次模拟考试数学试卷考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知双曲线C的两条渐近线的夹角为60°,则双曲线C的方程不可能为()A.B.C.D.2.如图是某地区2000年至2016年环境基础设施投资额(单位:亿元)的折线图.则下列结论中表述不正确的是()A.从2000年至2016年,该地区环境基础设施投资额逐年增加;B.2011年该地区环境基础设施的投资额比2000年至2004年的投资总额还多;C.2012年该地区基础设施的投资额比2004年的投资额翻了两番;D.为了预测该地区2019年的环境基础设施投资额,根据2010年至2016年的数据(时间变量t的值依次为)建立了投资额y与时间变量t的线性回归模型,根据该模型预测该地区2019的环境基础设施投资额为256.5亿元.3.一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的体积为()A.B.C.D.4.复数满足,则()A.B.C.D.5.设是定义域为的偶函数,且在单调递增,,则()A.B.C.D.6.已知集合,,则中元素的个数为()A.3B.2C.1D.07.已知命题:“关于的方程有实根”,若为真命题的充分不必要条件为,则实数的取值范围是()A.B.C.D.8.在中,内角所对的边分别为,若依次成等差数列,则()A.依次成等差数列B.依次成等差数列D.依次成等差数列C.依次成等差数列与抛物线相交于A,B两点,且A、B两点在抛物线准线上的投9.如图,已知直线影分别是M,N,若,则的值是()A.B.C.D.10.若是定义域为的奇函数,且,则A.的值域为B.为周期函数,且6为其一个周期C.的图像关于对称D.函数的零点有无穷多个11.已知函数满足当时,,且当时,;当时,且).若函数的图象上关于原点对称的点恰好有3对,则的取值范围是()A.B.C.D.12.已知定义在上的可导函数满足,若是奇函数,则不等式的解集是()A.B.C.D.二、填空题:本题共4小题,每小题5分,共20分。13.已知以x±2y=0为渐近线的双曲线经过点,则该双曲线的标准方程为________.14.正项等比数列满足,且成等差数列,则取得最小值时的值为_____15.已知函数为奇函数,,且与图象的交点为,,…,,则______.16.的展开式中的系数为__________(用具体数据作答).三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)已知函数,.(1)若曲线在点处的切线方程为,求,;(2)当时,,求实数的取值范围.18.(12分)△的内角的对边分别为,且.(1)求角的大小(2)若,△的面积,求△的周长.19.(12分)选修4-4:坐标系与参数方程:在平面直角坐标系中,曲线:(为参数),在以平面直角坐标系的原点为极点、轴的正半轴为极轴,且与平面直角坐标系取相同单位长度的极坐标系中,曲线:.(1)求曲线的普通方程以及曲线的平面直角坐标方程;(2)若曲线上恰好存在三个不同的点到曲线的距离相等,求这三个点的极坐标.20.(12分)如图,三棱柱ABC-A1B1C1中,侧面BCC1B1是菱形,AC=BC=2,∠CBB1=,点A在平面BCC1B1上的投影为棱BB1的中点E.(1)求证:四边形ACC1A1为矩形;的离心率为,右焦点为抛物线的焦点.(2)求二面角E-B1C-A1的平面角的余弦值.21.(12分)已知椭圆:(1)求椭圆的标准方程;(2)为坐标原点,过作两条射线,分别交椭圆于、两点,若、斜率之积为,求证:的面积为定值.22.(10分)如图,在四棱锥中,底面为菱形,底面,.(1)求证:平面;所成的角为,求平面(2)若直线与平面与平面所成锐二面角的余弦值.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、C【解析】判断出已知条件中双曲线的渐近线方程,求得四个选项中双曲线的渐近线方程,由此确定选项....