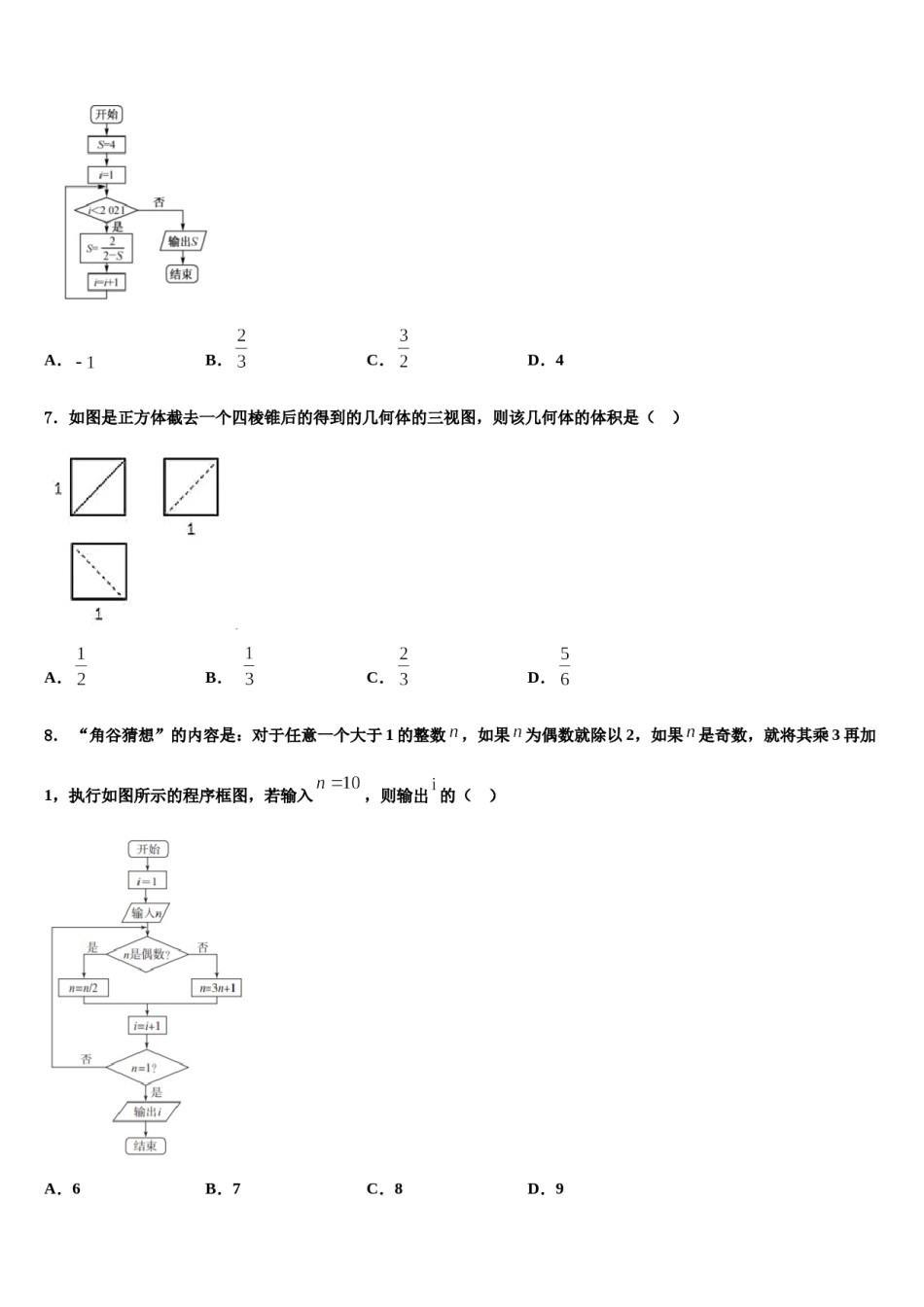
鄂尔多斯市第一中学2023-2024学年高三下学期联考数学试题请考生注意:1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知数列的前n项和为,,且对于任意,满足,则()A.B.C.D.2.已知实数,满足约束条件,则的取值范围是()A.B.C.D.3.已知双曲线的一个焦点为,且与双曲线的渐近线相同,则双曲线的标准方程为()A.B.C.D.4.已知等差数列中,,则()A.20B.18C.16D.145.若复数z满足,则()A.B.C.D.6.若执行如图所示的程序框图,则输出的值是()A.B.C.D.47.如图是正方体截去一个四棱锥后的得到的几何体的三视图,则该几何体的体积是()A.B.C.D.8.“角谷猜想”的内容是:对于任意一个大于1的整数,如果为偶数就除以2,如果是奇数,就将其乘3再加1,执行如图所示的程序框图,若输入,则输出的()A.6B.7C.8D.99.一小商贩准备用元钱在一批发市场购买甲、乙两种小商品,甲每件进价元,乙每件进价元,甲商品每卖出去件可赚元,乙商品每卖出去件可赚元.该商贩若想获取最大收益,则购买甲、乙两种商品的件数应分别为()A.甲件,乙件B.甲件,乙件C.甲件,乙件D.甲件,乙件10.已知函数,若,则的最小值为()参考数据:A.B.C.D.11.复数(为虚数单位),则等于()A.3B.D.C.2,点D在BC上,12.如图,中,将沿AD旋转得到三棱锥,分别记,与平面ADC所成角为,,则,的大小关系是()A.B.两种情况都存在D.存在某一位置使得C.,二、填空题:本题共4小题,每小题5分,共20分。13.函数的图象在处的切线方程为__________.14.三个小朋友之间送礼物,约定每人送出一份礼物给另外两人中的一人(送给两个人的可能性相同),则三人都收到礼物的概率为______.15.已知点是双曲线渐近线上的一点,则双曲线的离心率为_______16.已知全集,集合则_____.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)设数阵,其中、、、.设,其中,且.定义变换为“对于数阵的每一行,若其中有或,则将这一行中每个数都乘以;若其中没有且没有,则这一行中所有数均保持不变”(、、、).表示“将经过变换得到,再将经过变换得到、,以此类推,最后将经过变换得到”,记数阵中四个数的和为.(1)若,写出经过变换后得到的数阵;(2)若,,求的值;(3)对任意确定的一个数阵,证明:的所有可能取值的和不超过.18.(12分)已知函数与的图象关于直线对称.(为自然对数的底数)(1)若的图象在点处的切线经过点,求的值;(2)若不等式恒成立,求正整数的最小值.19.(12分)数列满足.(1)求数列的通项公式;(2)设,为的前n项和,求证:.20.(12分)已知中心在原点的椭圆的左焦点为,与轴正半轴交点为,且.时,直线(1)求椭圆的标准方程;(2)过点作斜率为、的两条直线分别交于异于点的两点、.证明:当过定点.,函数,其中为自然对数的底数.21.(12分)设(1)设函数.①若,试判断函数与的图像在区间上是否有交点;②求证:对任意的,直线都不是的切线;(2)设函数,试判断函数是否存在极小值,若存在,求出的取值范围;若不存在,请说明理由.22.(10分)已知函数.(Ⅰ)若是第二象限角,且,求的值;(Ⅱ)求函数的定义域和值域.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、D【解析】利用数列的递推关系式判断求解数列的通项公式,然后求解数列的和,判断选项的正误即可.【详解】当时,.所以数列从第2项起为等差数列,,所以,,.,,.故选:.【点睛】本题考查数列的递推关系式的应用、数列求和以及数列的通项公式的求法,考查转化思想以及计算能力,是中档题.2、B【解析】画出可行域,根据可行域上的点到原点距离,求得的取值范围.【详解】由约束条...