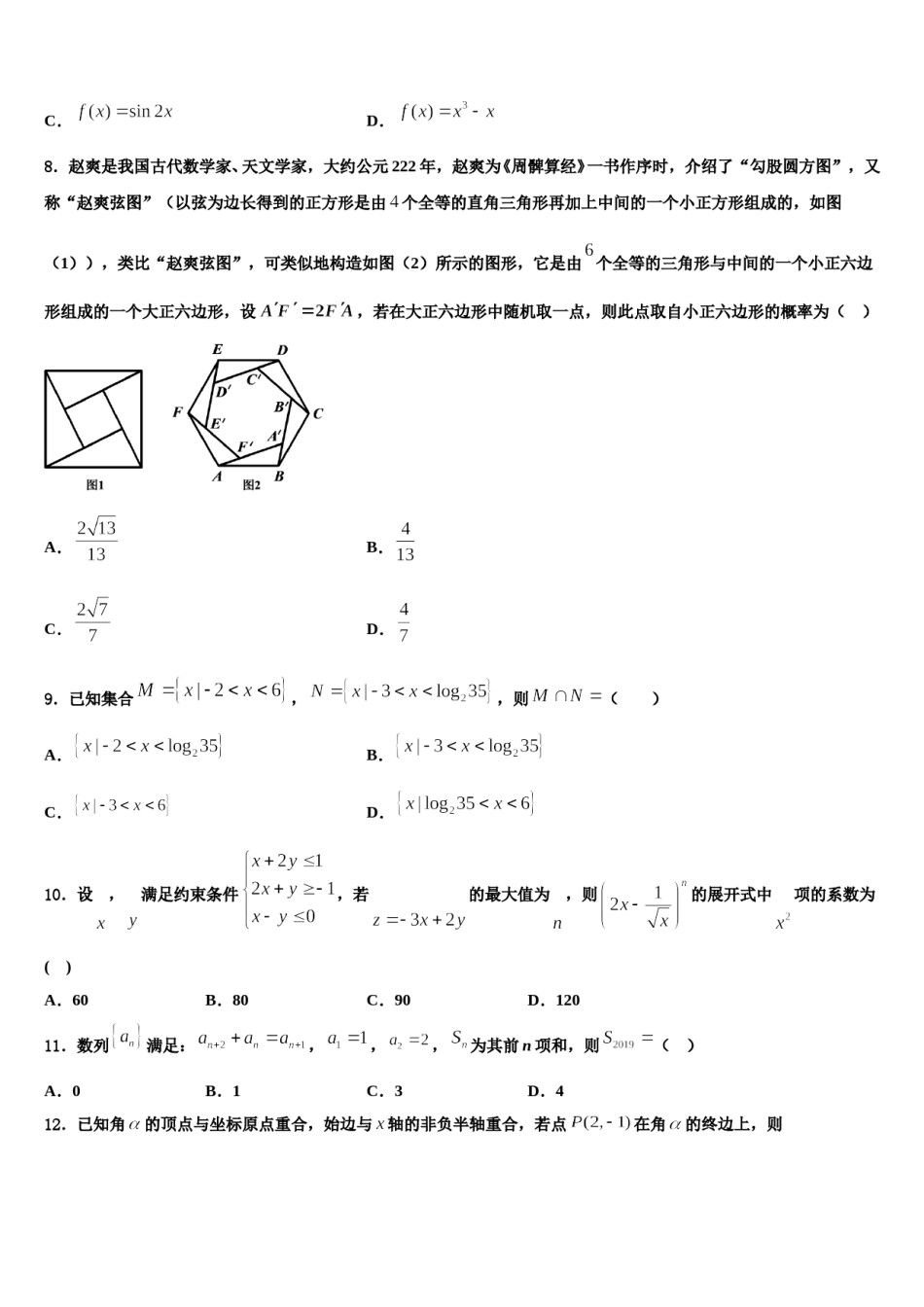
重庆市第八中学2023-2024学年高三六校第一次联考数学试卷注意事项铅笔作答;第二部分必须用黑1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知,椭圆的方程,双曲线的方程为,和的离心率之积为,则的渐近线方程为()A.B.C.D.2.已知函数是定义在上的偶函数,当时,,则,,D.的大小关系为()A.B.C.3.函数的图象如图所示,为了得到的图象,可将的图象()B.向右平移个单位A.向右平移个单位C.向左平移个单位D.向左平移个单位4.三棱锥的各个顶点都在求的表面上,且是等边三角形,底面,,,若点在线段上,且,则过点的平面截球所得截面的最小面积为()A.B.C.D.5.关于函数,有下述三个结论:①函数的一个周期为;②函数在上单调递增;③函数的值域为.其中所有正确结论的编号是()A.①②B.②C.②③D.③)6.某几何体的三视图如右图所示,则该几何体的外接球表面积为(A.B.C.D.7.下列函数中,既是奇函数,又在上是增函数的是().A.B.C.D.8.赵爽是我国古代数学家、天文学家,大约公元222年,赵爽为《周髀算经》一书作序时,介绍了“勾股圆方图”,又称“赵爽弦图”(以弦为边长得到的正方形是由个全等的直角三角形再加上中间的一个小正方形组成的,如图(1)),类比“赵爽弦图”,可类似地构造如图(2)所示的图形,它是由个全等的三角形与中间的一个小正六边形组成的一个大正六边形,设,若在大正六边形中随机取一点,则此点取自小正六边形的概率为()A.B.C.D.,则()9.已知集合,A.C.B.D.10.设,满足约束条件,若的最大值为,则的展开式中项的系数为()B.80C.90D.120A.6011.数列满足:,,,为其前n项和,则()在角的终边上,则A.0B.1C.3D.412.已知角的顶点与坐标原点重合,始边与轴的非负半轴重合,若点()A.B.C.D.,且与的等差中项为,则__________.二、填空题:本题共4小题,每小题5分,共20分。13.已知为等比数列,是它的前项和.若14.已知的展开式中含有的项的系数是,则展开式中各项系数和为______.15.一个四面体的顶点在空间直角坐标系中的坐标分别是,,,,则该四面体的外接球的体积为__________.16.已知数列的各项均为正数,记为数列的前项和,若,,则______.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)已知函数(1)解不等式;(2)若函数,若对于任意的,都存在,使得成立,求实数的取值范围.18.(12分)已知椭圆与x轴负半轴交于,离心率.(1)求椭圆C的方程;(2)设直线与椭圆C交于两点,连接AM,AN并延长交直线x=4于两点,若,直线MN是否恒过定点,如果是,请求出定点坐标,如果不是,请说明理由.,长轴的右端点与抛物线:的焦点重合,且椭19.(12分)如图,设椭圆:圆的离心率是.(Ⅰ)求椭圆的标准方程;面积的(Ⅱ)过作直线交抛物线于,两点,过且与直线垂直的直线交椭圆于另一点,求最小值,以及取到最小值时直线的方程.20.(12分)已知数列的前项和为,且点在函数的图像上;(1)求数列的通项公式;(2)设数列满足:,,求的通项公式;(3)在第(2)问的条件下,若对于任意的,不等式恒成立,求实数的取值范围;21.(12分)已知实数x,y,z满足,证明:.22.(10分)已知数列的前项和为,且满足.(1)求数列的通项公式;(2)若,,且数列前项和为,求的取值范围.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、A【解析】根据椭圆与双曲线离心率的表示形式,结合和的离心率之积为,即可得的关系,进而得双曲线的离心率方程.【详解】椭圆的方程,双曲线的方程为,则椭圆离心率,双曲线的离心率,由和的离心率之积为,即,解得,所以渐近线方程为,化简可得,故选:A.【点睛】本题考查了椭圆与双曲线简单几何性质应...