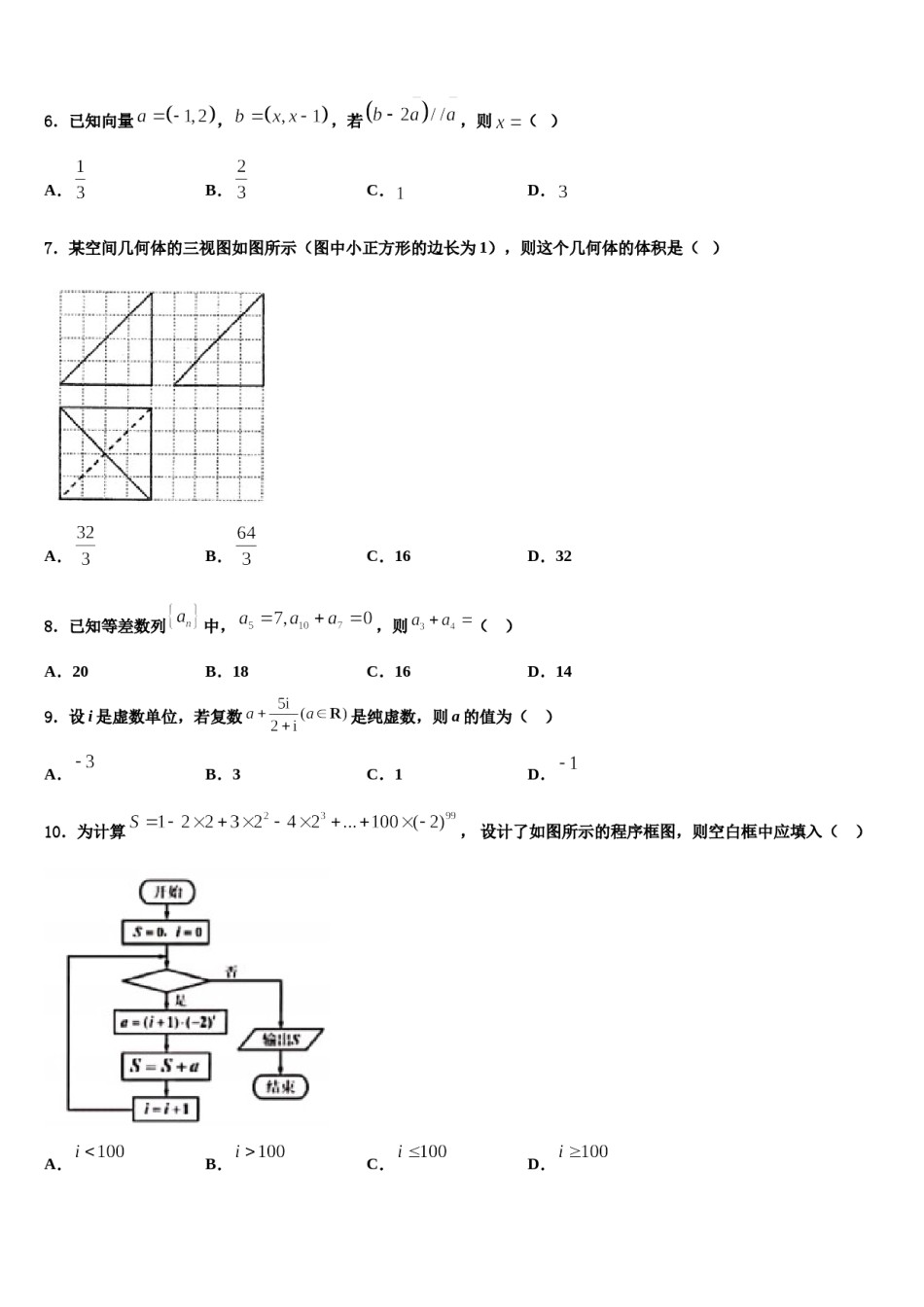
金学导航大联考2024届高三第三次模拟考试数学试卷注意事项铅笔作答;第二部分必须用黑1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.在中,内角A,B,C所对的边分别为a,b,c,D是AB的中点,若,且,则面积的最大值是()A.B.C.D.2.双曲线的离心率为,则其渐近线方程为A.B.C.D.3.已知平面向量,,满足:,,则的最小值为()A.5B.6C.7D.84.已知四棱锥的底面为矩形,底面,点在线段上,以为直径的圆过点.若,则的面积的最小值为()A.9B.7C.D.5.已知正项数列满足:,设,当最小时,的值为()A.B.C.D.6.已知向量,,若,则()A.B.C.D.7.某空间几何体的三视图如图所示(图中小正方形的边长为1),则这个几何体的体积是()A.B.C.16D.328.已知等差数列中,,则()A.20B.18C.16D.149.设i是虚数单位,若复数是纯虚数,则a的值为()A.B.3C.1D.10.为计算,设计了如图所示的程序框图,则空白框中应填入()A.B.C.D.11.已知集合,则=()A.B.C.D.12.某四棱锥的三视图如图所示,则该四棱锥的表面积为()A.8B.C.D.的最小值为___________.二、填空题:本题共4小题,每小题5分,共20分。13.已知,,,且,则14.已知双曲线-=1(a>0,b>0)与抛物线y2=8x有一个共同的焦点F,两曲线的一个交点为P,若FP=5,则点F到双曲线的渐近线的距离为_____.15.已知复数,其中为虚数单位,则的模为_______________.16.已知正数a,b满足a+b=1,则的最小值等于__________,此时a=____________.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)如图,三棱台中,侧面与侧面是全等的梯形,若,且.(Ⅰ)若,,证明:∥平面;(Ⅱ)若二面角为,求平面与平面所成的锐二面角的余弦值.18.(12分)已知函数.(1)若曲线存在与轴垂直的切线,求的取值范围.(2)当时,证明:.19.(12分)已知函数,为的导数,函数在处取得最小值.(1)求证:;(2)若时,恒成立,求的取值范围.20.(12分)已知函数.若在定义域内存在,使得成立,则称为函数的局部对称点.且a≠0,证明:函数有局部对称点;(1)若a,(2)若函数在定义域内有局部对称点,求实数c的取值范围;(3)若函数在R上有局部对称点,求实数m的取值范围.21.(12分)已知数列,满足.(1)求数列,的通项公式;(2)分别求数列,的前项和,.22.(10分)已知等差数列和等比数列满足:(I)求数列和的通项公式;(II)求数列的前项和.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、A【解析】根据正弦定理可得,求出,根据平方关系求出.由两端平方,求的最大值,根据三角形面积公式,求出面积的最大值.【详解】,中,由正弦定理可得,整理得,由余弦定理,得.D是AB的中点,且,,即,即,,当且仅当时,等号成立.的面积,所以面积的最大值为.故选:.【点睛】本题考查正、余弦定理、不等式、三角形面积公式和向量的数量积运算,属于中档题.2、A【解析】分析:根据离心率得a,c关系,进而得a,b关系,再根据双曲线方程求渐近线方程,得结果.详解:因为渐近线方程为,所以渐近线方程为,选A.点睛:已知双曲线方程求渐近线方程:.3、B的最小值转化为用该关系式表达的算式,【解析】建立平面直角坐标系,将已知条件转化为所设未知量的关系式,再将利用基本不等式求得最小值.【详解】,,且,由于建立平面直角坐标系如下图所示,设.所以.,所以.,即.当且仅当时取得最小值,此时由得,当时,有最小值为,即,,解得.所以当且仅当时有最小值为.故选:B【点睛】本小题主要考查向量的位置关系、向量的模,考查基本不等式的运用,考查数形结合的数学思想方法,属于难题.4、C【解析】根据线面垂直的性质以及线面垂直的判定,根据勾股定理,得到之间的等量关...