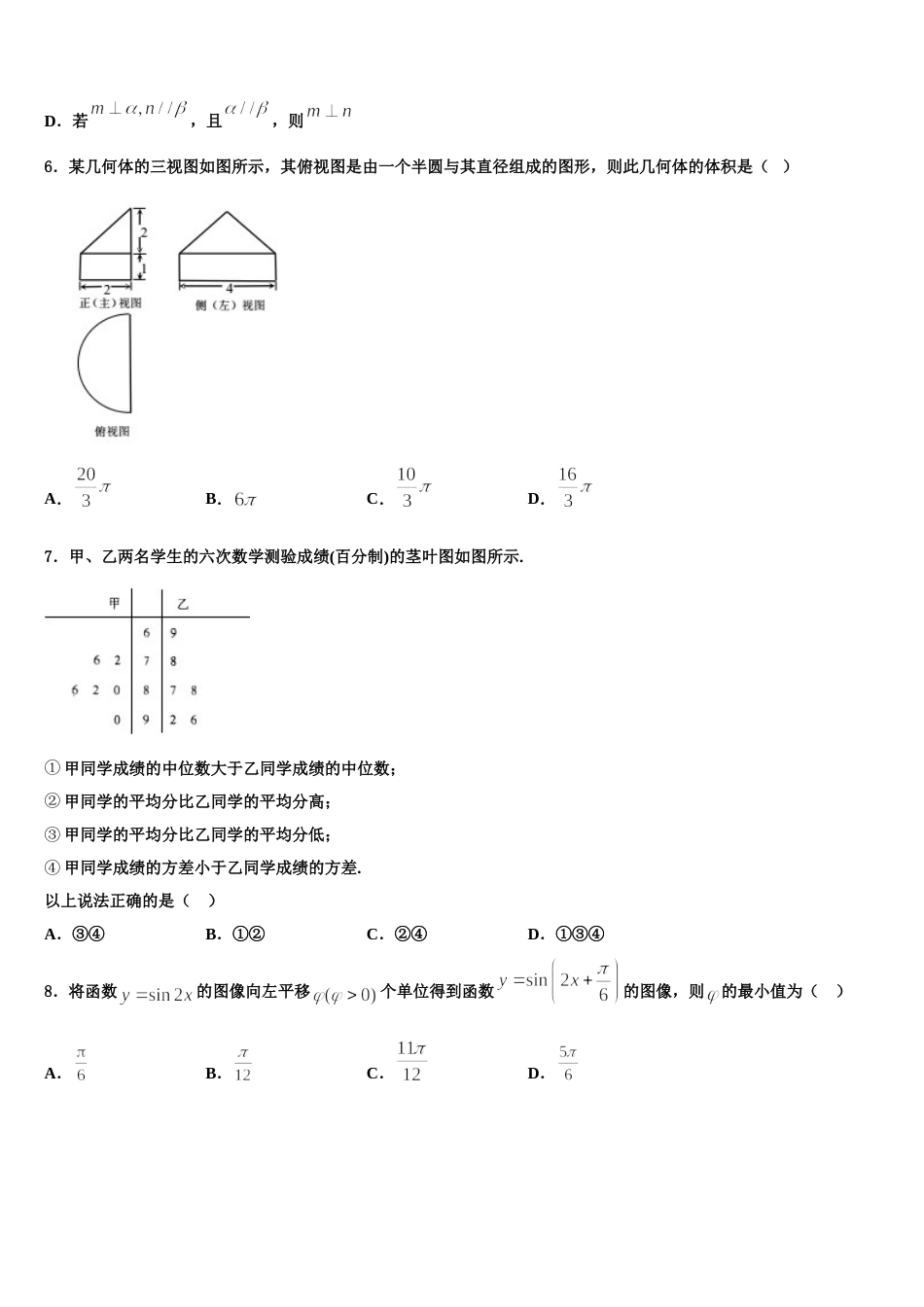
陕西省兴平市秦岭中学 2023-2024 学年高考压轴卷数学试卷考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.中国古代数学著作《算法统宗》中有这样一个问题;“三百七十八里关,初行健步不为难,次后脚痛递减半,六朝才得到其关,要见每朝行里数,请公仔细算相还.”其意思为:“有一个人走了 378 里路,第一天健步走行,从第二天起脚痛每天走的路程是前一天的一半,走了 6 天后到达目的地,求该人每天走的路程.”由这个描述请算出这人第四天走的路程为( )A.6 里B.12 里C.24 里D.48 里2.已知直线 :过双曲线的一个焦点且与其中一条渐近线平行,则双曲线的方程为( )A.B.C.D.3.若复数在复平面内对应的点在第二象限,则实数的取值范围是( )A.B.C.D.4.已知角的顶点与原点重合,始边与轴的正半轴重合,终边经过点,则( )A.B.C.D.5.已知是空间中两个不同的平面,是空间中两条不同的直线,则下列说法正确的是( )A.若,且,则B.若,且,则C.若,且,则D.若,且,则6.某几何体的三视图如图所示,其俯视图是由一个半圆与其直径组成的图形,则此几何体的体积是( )A.B.C.D.7.甲、乙两名学生的六次数学测验成绩(百分制)的茎叶图如图所示.① 甲同学成绩的中位数大于乙同学成绩的中位数;② 甲同学的平均分比乙同学的平均分高;③ 甲同学的平均分比乙同学的平均分低;④ 甲同学成绩的方差小于乙同学成绩的方差.以上说法正确的是( )A.③④B.①②C.②④D.①③④8.将函数的图像向左平移个单位得到函数的图像,则的最小值为( )A.B.C.D.9.若,满足约束条件,则的最大值是( )A.B.C.13D.10.已知是过抛物线焦点的弦,是原点,则( )A.-2B.-4C.3D.-311.已知等差数列的公差为-2,前项和为,若,,为某三角形的三边长,且该三角形有一个内角为,则的最大值为( )A.5B.11C.20D.2512.不等式的解集记为,有下面四个命题:;;;.其中的真命题是( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知等差数列的前项和为,且,则______.14.过动点作圆:的切线,其中为切点,若(为坐标原点),则的最小值是__________.15.设随机变量服从正态分布,若,则的值是______.16.为了抗击新型冠状病毒肺炎,某医药公司研究出一种消毒剂,据实验表明,该药物释放量与时间的函数关系为(如图所示),实验表明,当药物释放量对人体无害. (1)______;(2)为了不使人身体受到药物伤害,若使用该消毒剂对房间进行消毒,则在消毒后至少经过______分钟人方可进入房间.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)如图,在四棱锥中,平面平面,.(Ⅰ)求证:平面;(Ⅱ)若锐二面角的余弦值为,求直线与平面所成的角.18.(12 分)在四棱锥中,底面为直角梯形,,,,,,,分别为,的中点.(1)求证:.(2)若,求二面角的余弦值.19.(12 分)在直角坐标系中,直线 l 过点,且倾斜角为,以直角坐标系的原点 O 为极点,x轴的正半轴为极轴建立极坐标系,曲线 C 的极坐标方程为.求直线 l 的参数方程和曲线 C 的直角坐标方程,并判断曲线 C 是什么曲线;设直线 l 与曲线 C 相交与 M,N 两点,当,求的值.20.(12 分)已知函数有两个零点.(1)求的取值范围;(2)是否存在实数, 对于符合题意的任意,当 时均有?若存在,求出所有的值;若不存在,请说明理由.21.(12 分)已知矩阵,,若矩阵,求矩阵的逆矩阵.22.(10 分)在综合素质评价的某个维度的测评中,依据评分细则,学生之间相互打分,最终将所有的数据合成一个分数,满分 100 分...