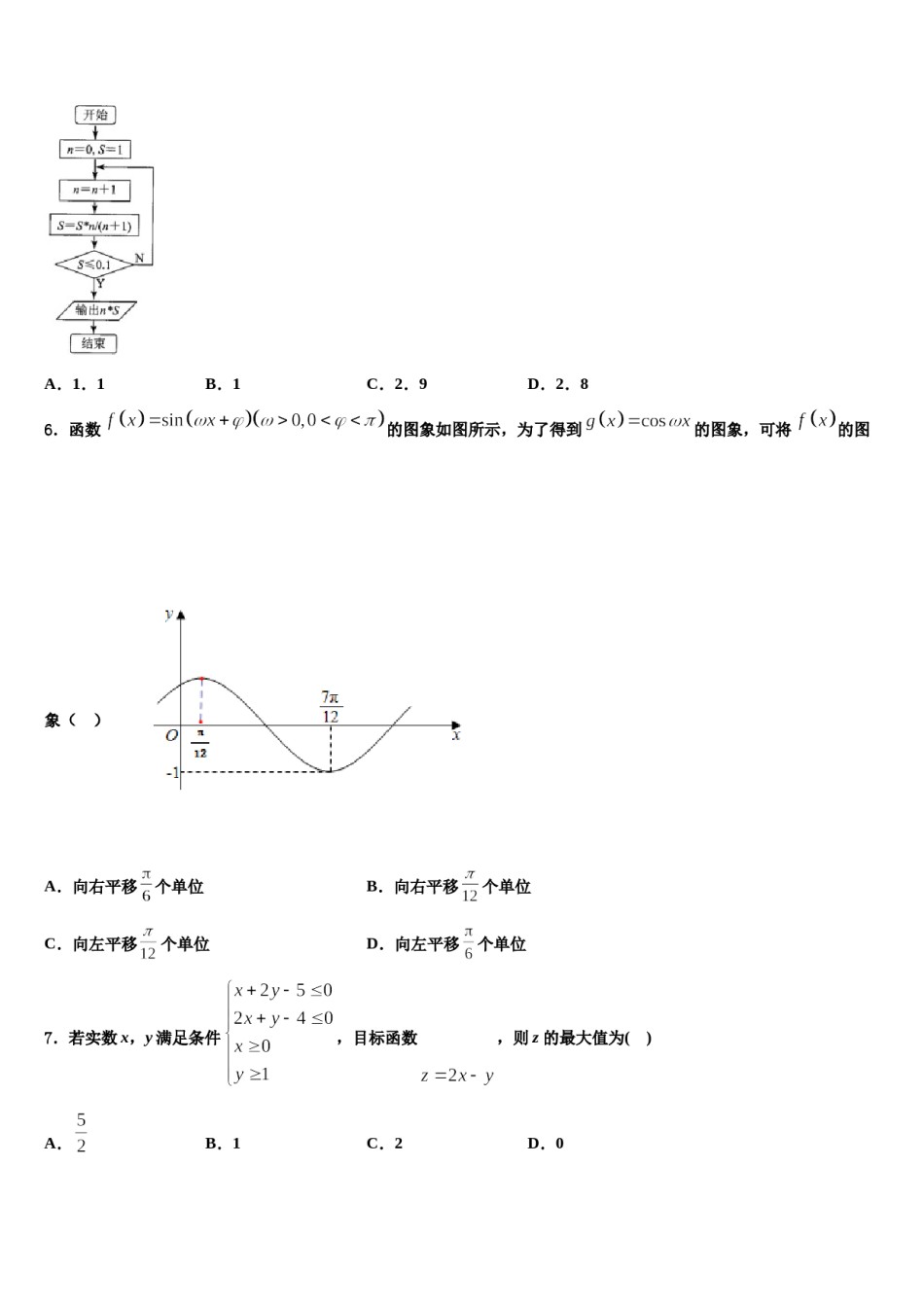
黑龙江省哈尔滨市名校2024年高考压轴卷数学试卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.某部队在一次军演中要先后执行六项不同的任务,要求是:任务A必须排在前三项执行,且执行任务A之后需立即执行任务E,任务B、任务C不能相邻,则不同的执行方案共有()A.36种B.44种C.48种D.54种2.函数在上单调递减,且是偶函数,若,则的取值范围是()B.(﹣∞,1)∪(2,+∞)A.(2,+∞)D.(﹣∞,1)C.(1,2)3.下列命题是真命题的是()A.若平面,,,满足,,则;B.命题:,,则:,;C.“命题为真”是“命题为真”的充分不必要条件;D.命题“若,则”的逆否命题为:“若,则”.4.某三棱锥的三视图如图所示,那么该三棱锥的表面中直角三角形的个数为()A.1B.2C.3D.05.阅读下面的程序框图,运行相应的程序,程序运行输出的结果是()A.1.1B.1C.2.9D.2.86.函数的图象如图所示,为了得到的图象,可将的图象()A.向右平移个单位B.向右平移个单位C.向左平移个单位D.向左平移个单位7.若实数x,y满足条件,目标函数,则z的最大值为()A.B.1C.2D.08.集合的子集的个数是()A.29.函数B.3C.4D.8满足对任意都有成立,且函数的图象关于点对称,,则B.2的值为()D.1A.0C.410.抛物线的焦点为,准线为,,是抛物线上的两个动点,且满足,设线段的中点在上的投影为,则的最大值是()A.B.C.D.11.已知f(x)=是定义在R上的奇函数,则不等式f(x-3)<f(9-x2)的解集为()A.(-2,6)B.(-6,2)C.(-4,3)D.(-3,4)12.已知集合,集合,则等于()A.B.C.D.二、填空题:本题共4小题,每小题5分,共20分。13.已知抛物线的焦点为,斜率为2的直线与的交点为,若,则直线的方程为___________.经过抛物线E:的焦点,则抛物线E的准线与圆C相交所得弦长是_14.已知圆C:_________.15.已知数列满足,且恒成立,则的值为____________.16.对定义在上的函数,如果同时满足以下两个条件:(1)对任意的总有;(2)当,,时,总有成立.则称函数称为G函数.若是定义在上G函数,则实数a的取值范围为________.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)已知函数,.(1)若不等式的解集为,求的值.(2)若当时,,求的取值范围.18.(12分)已知关于的不等式有解.(1)求实数的最大值;(2)若,,均为正实数,且满足.证明:.19.(12分)已知函数(是自然对数的底数,).(1)求函数的图象在处的切线方程;(2)若函数在区间上单调递增,求实数的取值范围;(3)若函数在区间上有两个极值点,且恒成立,求满足条件的的最小值(极值点是指函数取极值时对应的自变量的值).20.(12分)设抛物线的焦点为,准线为,为抛物线过焦点的弦,已知以为直径的圆与相切于点.(1)求的值及圆的方程;(2)设为上任意一点,过点作的切线,切点为,证明:.21.(12分)某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数x与烧开一壶水所用时间y的一组数据,且作了一定的数据处理(如表),得到了散点图(如图).表中,.(1)根据散点图判断,与哪一个更适宜作烧水时间y关于开关旋钮旋转的弧度数x的回归方程类型?(不必说明理由)(2)根据判断结果和表中数据,建立y关于x的回归方程;(3)若旋转的弧度数x与单位时间内煤气输出量t成正比,那么x为多少时,烧开一壶水最省煤气?附:对于一组数据,,,…,,其回归直线的斜率和截距的最小二乘估计分别为,.22.(10分)已知,,且.(1)求的最小值;(2)证明:.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、B...